
Eine der wichtigsten Metriken in der allgemeinen Relativitätstheorie ist die Schwarzschildmetrik. Sie beschreibt, wie der Raum um eine kugelförmige Massenverteilung herum gekrümmt ist. Es ist wichtig sich klar zu machen, dass die Schwarzschildmetrik streng nur im massenfreien Raum, also außerhalb jeder Masse und nur für nicht rotierende Körper gilt. Sie ist aber auch bei nicht ganz kugelsymmetrischen, langsam rotierenden Körpern, wie die Erde oder die Sonne eine gute Näherung.
Da die Schwarzschildmetrik für kugelsymmetrische Körper gilt, wird sie fast immer in Kugelkoordinaten angegeben. Zum Vergleich ist es daher sinnvoll, zunächst die Metrik des ungekrümmten Raums in Kugelkoordiaten anzugeben:

Dies ist die Minkowski-Metrik in Kugelkoordinaten.
Befindet sich ein Objekt nun in einem Schwerkraft-Feld, so läuft die Eigenzeit um so langsamer, je näher das Objekt dem Massenzentrum kommt. Zudem ist auch der Raum verzerrt, so dass ein lokaler Beobachter nicht die Abstände misst, die man in Kugelkoordinaten des ungekrümmten Raumes erwarten würde.
So wie man den ungekrümmten Raum der speziellen Relativitätstheorie mit verschiedenen Koordinaten darstellen kann, zum Beispiel in Kartesischen Koordinaten oder in den hier angegebenen Kugelkoordinaten, kann man auch in der allgemeinen Relativitätstheorie den Raum mit unterschiedlichen Koordinaten darstellen. Die Schwarzschildmetrik lässt sich also in verschiedenen Formen angeben, die sich hauptsächlich in der Art, wie sie die Raumachsen definieren, unterscheiden.
In der Standardform der Schwarzschildmetrik wird die Radiuskoordinate r so definiert, dass der Umfang um die Kugel mit dieser Radiuskoordinaten gerade 2πr ergibt. Das führt dazu, dass die Winkelkoordinaten φ und θ unverzerrt bleiben und die Raumkrümmung sich nur auf die Radialkoordinate auswirkt.
Die Standardform der Schwarzschildmetrik lautet unter dieser Voraussetzung:
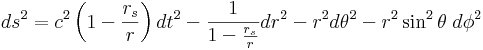
mit dem Schwarzschildradius rs von

Der Vergleich mit der Minkowski-Metrik in Kugelkoordinaten zeigt sofort, dass sich die Vorfaktoren von den Winkelkoordinaten nicht geändert haben. Die Änderung des Winkels θ um eine kleine Einheit entspricht auch hier einer Abstandsänderung von r mal dieser Einheit. Die Änderung der Zeitkoordinate entspricht jedoch einer um so kleineren Änderung der Eigenzeit, je näher man dem Zentrum kommt. Die Zeit im Gravitationsfeld ist verlangsamt. Im Gegensatz dazu entspricht eine Änderung der Radialkoordinate einer immer größeren Abstandsänderung, je näher man dem Zentrum kommt. Der Raum ist gedehnt.
Am Schwarzschildradius rs wird die Metrik singulär: Der Faktor vor der Zeitkomponente wird null und der Faktor für die Radialkomponente wird unendlich. Tatsächlich ist das nur eine Eigenart dieses Koordinatensystems. Dieses ist nur für Radien größer als rs anwendbar.
Der Abstand d von einem Beobachter am Radius r1 zum Ereignishorizont errechnet sich zu:

Dieser Abstand ist zwar immer größer als r1-rs, aber er ist nicht unendlich. Der Schwarzschildradius befindet sich also für einen äußeren Beobachter durchaus in einer wohl definierten Entfernung.
Das besondere an der allgemeinen Relativitätstheorie ist, dass ihre Formulierung von der konkreten Wahl des Koordinatensystems unabhängig ist. Man kann die selbe physikalische Situation in verschiedenen Koordinatensystemen darstellen.
Eine Alternative zur Darstellung der Schwarzschildmetrik in Standard-Koordinaten sind die isotropen Koordinaten. Oben habe ich ausgeführt, dass in Standard-Koordinaten der Radius r gedehnt und die Zeit t verlangsamt ist. Die Winkelkoordinaten θ und φ werden dagegen nicht berührt. In isotropen Koordinaten wird nun die Radiuskoordinate so definiert dass Radius und Winkelkoordinaten gleichartig gedehnt erscheinen. Man geht also vom Standard-Radius r in eine neue Radiuskoordinate ρ über. Die Transformationsformel lautet:
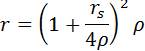
Setzt man das neue ρ jetzt in die Schwarzschildmetrik ein, so erhält man neue koeffizienten in allen Koordinaten, weil überall die Radiuskoordinate r durch obigen Ausdruck ersetzt werden muss. Man erhält die Schwarzschildmetrik in isotropen Koordinaten:

In dieser Form der Metrik liegt die zeitliche Singularität beim Radius

und nicht nur die Radius-Komponente ist gedehnt, sondern alle Raumkomponenten gleichermaßen um den Faktor
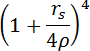
Die Koordinaten heißen isotrop, weil jetzt nicht mehr nur der Radiusvektor gegenüber den euklidischen Kugelkoordinaten gedehnt ist, sondern der Raum in alle Richtungen der gleichen Dehung ausgesetzt ist. Isotrop bedeutet richtungsunabhängig. In diesen Koordinaten sind die Richtungen in ρ, θ und φ weitgehend gleichberechtigt. ρ unterscheidet sich von den anderen räumlichen Koordinaten nur noch dadurch, dass sich in diese Richtung die Zeitverlangsamung ändert.
Letzte Änderung: 28.11.2013
© Joachim Schulz